InnoDB一棵B+树能存储多少行数据 原理分析与计算
引言
在MySQL后端开发面试中,"InnoDB一棵B+树可以存放多少行数据"是一个经典的技术问题。这个问题不仅考察候选人对InnoDB存储引擎的理解深度,还涉及到数据库性能优化、索引设计等核心知识。本文将深入分析这个问题的计算逻辑和技术细节。
B+树与InnoDB存储结构
B+树的基本概念
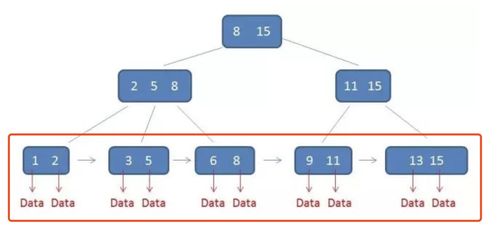
InnoDB使用B+树作为其索引结构,这是一种平衡多路搜索树,具有以下特点:
- 所有数据都存储在叶子节点
- 非叶子节点仅存储索引键值和指向子节点的指针
- 叶子节点之间通过指针连接,支持范围查询
InnoDB页结构
InnoDB中数据存储的基本单位是"页"(Page),默认大小为16KB。每个页包含:
- 页头(38字节):存储控制信息
- 行记录:实际的数据行
- 页目录(Slots):加速页内记录查找
- 页尾(8字节):校验信息
计算一棵B+树能存储多少行数据
关键参数
计算需要考虑以下几个关键参数:
- 页大小:默认16KB(16384字节)
- 非叶子节点指针大小:6字节
- 主键大小:假设为8字节(BIGINT)
- 行记录大小:根据实际表结构而定
计算步骤
1. 计算非叶子节点能存储的指针数量
每个非叶子节点条目包含:主键值 + 子节点指针
- 每个条目大小 = 8字节(主键) + 6字节(指针) = 14字节
- 可用空间 ≈ 16KB - 页头页尾 ≈ 16200字节
- 每个节点最大条目数 ≈ 16200 ÷ 14 ≈ 1157
2. 计算叶子节点能存储的行数
假设行记录平均大小为1KB(包含行头、字段数据等):
- 可用空间 ≈ 16200字节
- 每个叶子节点行数 ≈ 16200 ÷ 1024 ≈ 15行
3. 计算B+树总容量
- 第一层(根节点):1个节点
- 第二层:最多1157个节点
- 第三层:最多1157² ≈ 1,338,649个节点
- 叶子节点:最多1157³ ≈ 1,548,000,000个节点
总行数 = 叶子节点数 × 每页行数
= 1,548,000,000 × 15 ≈ 23,220,000,000行
影响因素分析
1. 主键大小
如果使用4字节的INT作为主键:
- 每个非叶子节点条目大小 = 4 + 6 = 10字节
- 每个节点最大条目数 ≈ 16200 ÷ 10 ≈ 1620
- 总行数将大幅增加
2. 行记录大小
行记录大小直接影响存储密度:
- 小行记录(200字节):每页可存储约80行
- 大行记录(8KB):每页只能存储约2行
3. 填充因子
实际存储时需要考虑页的填充因子,通常不会完全填满,以预留空间用于更新操作。
实际应用意义
性能优化
理解B+树容量有助于:
- 合理设计表结构,控制行大小
- 选择合适的索引策略
- 预估数据增长趋势
- 制定分库分表策略
索引设计
- 主键应尽可能小,以增加B+树的扇出
- 避免过度索引,减少存储开销
- 考虑复合索引的前缀选择性
总结
一棵InnoDB B+树理论上可以存储数十亿行数据,但实际容量受到多种因素影响:
- 主键大小
- 行记录大小
- 页填充因子
- 索引结构设计
在实际应用中,当单表数据量接近B+树的理论上限时,应考虑分库分表、归档等策略,以维持数据库的性能和可维护性。深入理解这些原理,对于后端开发人员设计高性能数据库系统至关重要。
如若转载,请注明出处:http://www.somaodata.com/product/34.html
更新时间:2025-11-28 12:16:59